More Emacs - a better eshell
Some Emacs users live their entire lives without ever meeting eshell. Eshell is a command-line shell where you can run programs, list directories, copy files and do all kinds of things you would normally need a terminal window for. Eshell even made a cameo appearance in Tron Legacy, as the command-line interface to Encom's computers. Unfortunately, there is something it won't do: it's not easy to start more than one eshell session - when you invoke eshell for the second time, it goes back to the buffer the first eshell opened, normally called "*eshell*". I could invoke the "rename-uniquely" command manually after opening each eshell window (or before attempting to open a new one), but that's annoying (and I ofen forget it).
I keep eshell bound to C-$ (control-$ for the emacs-illiterate ou ^$ for really old-school folks - not that any keyboard I know of emits valid ASCII when someone presses Control-$). I often need more than one shell. "ansi-term" will do the buffer-renaming magic and I can start a number of those, but that's not really what I want - ansi-term runs the shell as a separate process. I use it when I need things I'd need another terminal for, like input and output redirection, but I'd prefer to use eshell when all I need is another shell.
Unfortunate people who don't use Emacs will think I would need to dig up the sources of eshell to add the rename-uniquely invocation and change them. I'll remind those poor folks than your init.el file is, in fact, executed when Emacs starts and, therefore, all I need to do is to change my binding from
(global-set-key (kbd "C-$") 'eshell)
to
(global-set-key (kbd "C-$") '(lambda () (interactive) (eshell) (rename-uniquely) ))
In case you are wondering, the "interactive" function is invoked to mark this function as a command. If I didn't do it (as I foolishly did earlier this morning, before reading this) I'd be greeted with
Wrong type argument: commandp, (lambda nil (eshell) (rename-uniquely))
That's nice, but not perfect. If you invoke it, you will notice your first eshell buffer is named "*eshell*<2>". That's bad.
It happens because the buffer is uniquely renamed every time it's created, not only when there already is a buffer named "*eshell*". For that, we need a little more code:
(global-set-key (kbd "C-$") '(lambda () (interactive) (if (member "*eshell*" (mapcar* 'buffer-name (buffer-list))) (progn (eshell) (rename-uniquely)) (eshell))))
OK. That was stupid. We test whether there is already a buffer named "*eshell*" and then we try to invoke eshell to create a new one, forgetting that eshell will also find the buffer called "*eshell*" and switch to it rather than creating a new one. We then, dumbly, rename our only eshell buffer.
This thing needs more brains.
Since I don't expect to have more than a handful eshells running (you really shouldn't try to), progressing through numbered buffer names until we find a free one should be a fine approach:
(global-set-key (kbd "C-$") '(lambda ()
(interactive)
(let ((i 1)
(found-a-name nil))
(while (not found-a-name)
(setq buffname
(concat "*eshell*<" (int-to-string i) ">"))
(setq found-a-name (not (member buffname
(mapcar* 'buffer-name
(buffer-list)))))
(if found-a-name
(eshell i)
(setq i (+ i 1))
)))))
Now we start from i = 1 and check if there is already a buffer named "*eshell*<i>". If there is not, create one with that name (passing the number to eshell) and end our search. This is doubly pretty, because the first solution would rename our first eshell as "*eshell*<2>". With this one, the first eshell is "*eshell*<1>", which is elegant. If you manually open an eshell, it'll be called "*eshell*", distinguishing it from our automatically named shells.
Still, as a friend of mine well pointed out, the code is really ugly. It'll also fail if the default name for eshell buffers is changed. In short, it's a mess. I felt compelled to do better:
(global-set-key (kbd "C-$") '(lambda () (interactive) (let ((i 1)) (while (member (concat eshell-buffer-name "<" (int-to-string i) ">") (mapcar* 'buffer-name (buffer-list))) (setq i (+ 1 i))) (eshell i))))
Much more concise and to-the-point. I like it.
Can you customize Eclipse like that?
A bug. Yes, they hit me too
After publishing this, I noticed the variable eshell-buffer-name is not defined until after you invoke eshell for the first time. If you try to C-$ on a freshly started Emacs session, you'll get a
Symbol's value as variable is void: eshell-buffer-name
message. In order to fix this, the code must check whether eshell-buffer-name is bound and, if it's not, we start the buffer giving it a 1.
(global-set-key (kbd "C-$") '(lambda () (interactive) (let ((i 1)) (if (boundp 'eshell-buffer-name) (progn (while (member (concat eshell-buffer-name "<" (int-to-string i) ">") (mapcar* 'buffer-name (buffer-list))) (setq i (+ 1 i))) (eshell i)) (eshell 1)))) )
OK. Now I am satisfied.
Edit: And now, I feel stupid
A friend of mine, very politely, possibly to avoid embarrassing me in public, sent me an e-mail pointing out he didn't quite understood what I was trying to accomplish here. In his message, he pointed out I could just invoke (eshell t). When passed "t" (boolean true in Lisp) as a parameter, eshell does precisely what I wanted it to do. So, the new version in my init.el is even shorter:
(global-set-key (kbd "C-$") '(lambda () (interactive) (eshell t)))
Well... At least I learned something.
Emacs perfection - selecting fonts according to screen size
Most of the time, I work at my desk, where my netbook is hooked up to a reasonably sized monitor (the largest its feeble GPU can handle with acceleration). Since screen real-estate in that situation is abundant, I opted to use a larger font (one I made from the x3270 bitmap font, but that's another, much longer story). Unfortunately, when I am not at my desk, the 1024x600 LCD is quite limiting and the default options don't work for me. When I am away from the big screen monitor, screen real-estate is limited and a small font should be selected by default.
I started from the options the Custom menu gave me. Removing comments, it's a very simple snippet:
(custom-set-faces
'(default ((t (:inherit nil :stipple nil :inverse-video nil :box nil :strike-through nil :overline nil
:underline nil :slant normal :weight normal :height 140 :width normal :family "IBM 3270"))))
'(linum ((t (:inherit default :foreground "#777" :height 110)))))
Translating that to English, I have a font called "IBM 3270" at a 14-point height, with line numbers with 11 points. Very readable.
But that doesn't solve the problem when I am on the road.
The friendly guys at Stack Overflow pointed out one way to do it: x-display-pixel-width and x-display-pixel-height.
With that in hand, I can do:
(if (> (x-display-pixel-width) 1280)
; screen is big
(custom-set-faces
'(default ((t (:inherit nil :stipple nil :inverse-video nil :box nil :strike-through nil :overline nil
:underline nil :slant normal :weight normal :height 140 :width normal :family "IBM 3270"))))
'(linum ((t (:inherit default :foreground "#777" :height 110)))))
; screen is small
(custom-set-faces
'(default ((t (:inherit nil :stipple nil :inverse-video nil :box nil :strike-through nil :overline nil
:underline nil :slant normal :weight normal :height 110 :width normal :family "IBM 3270"))))
'(linum ((t (:inherit default :foreground "#777" :height 80)))))
)
and I can be happy.
But can I?
When I start Emacs without X (as in from a remote terminal), these functions issue an ugly warning telling me that X is not available and that I should --debug-init and fix the problem. That's safely ignorable (as these adjustments are being done when everything non-cosmetic is already in place, at least in my init.el), but, still, annoying.
There is a variable, window-system, that can help - it holds "x" if we are under the X windowing system and nil if we are using a character terminal. With it, I can do:
(if (and (eq 'x window-system) (> (x-display-pixel-width) 1280))
; screen is big
(custom-set-faces
'(default ((t (:inherit nil :stipple nil :inverse-video nil :box nil :strike-through nil :overline nil
:underline nil :slant normal :weight normal :height 140 :width normal :family "IBM 3270"))))
'(linum ((t (:inherit default :foreground "#777" :height 110)))))
; screen is small
(custom-set-faces
'(default ((t (:inherit nil :stipple nil :inverse-video nil :box nil :strike-through nil :overline nil
:underline nil :slant normal :weight normal :height 110 :width normal :family "IBM 3270"))))
'(linum ((t (:inherit default :foreground "#777" :height 80)))))
)
short-circuiting the x-display-pixel-width and allowing Emacs starts cleanly from a remote terminal session. Since window-system also can tell you if you are on a Mac (or NeXT, if you are into retrocomputing) or under Windows (you can't argue taste), you can take appropriate actions according to your environment.
I am happy for today.
An Emacs cheatsheet as a mindmap
I have been using Emacs for some time now. It has a very steep learning curve, but its power and elegance make it my editor of choice for just about everything. So, inspired by this article, I decided to create my own Emacs cheatsheet. There are many Emacs cheatsheets, but all of them use a tabular format that is not, in my noob opinion, the best way to convey such information: you can interpret the Emacs commands as a tree-like keystroke structure and many important commands use two or more steps.
I started a mind-map for the keystroke trees with the commands I use the most (and some of the ones I find the most amusing). The plan is to make a navigable cheat sheet like the Mercurial and Git ones you can get here and here, plus some tips on what to add to your ~/emacs.d/init.el file.
You can get the very, very early version of the mind-map (in Freemind format) here or just look into the image that follows.
All the heavy magic is also missing, like the "smart paste" Marco Baringer does about 1:45 into the What is Ajax screencast that relates to the David Crane's Ajax in Action
book (that I still don't know how is done).
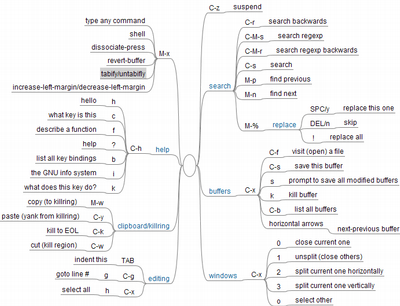
I would appreciate any advice from Emacs veterans and newbies alike, so, feel free to comment.
Editor nirvana
To say GNU Emacs is merely a text editor is an understatement. Ever since I decided I would learn to use it (out of a never quite accomplished mission of learning Lisp once and for all), it impresses me almost on a daily basis.
Yesterday, while playing with my choice of screen fonts for the editor (something every bit as important as choosing one's text editor), I discovered two pop-up menu options, to increase and decrease font size. A little playing with Meta-X and I arrived a couple functions, "text-scale-increase" and "text-scale-decrease". A little more digging brought me to the key combinations "Control X Control plus" and "Control X Control minus" sequences. Usable, but I wanted something easier to type.
Few non-Emacs users appreciate the fact Emacs has no configuration file. What it has is a program, in its own Lisp dialect, that's executed every time the editor is started. Within this program I can define new functions, load external libraries and even write a credible implementation of vi. This time I made two simple edits to my init.el file that added two new key bindings:
(global-set-key (kbd "C--") 'text-scale-decrease) (global-set-key (kbd "C-+") 'text-scale-increase)
The first one binds the "Control minus" key combination to the text-scale-decrease function (that decreases text size) while the second binds "Control plus" to the opposite text-scale-increase function. Easy enough for me. Now, every time Emacs starts, it has a couple bindings extra key bindings (on top of all other already added by loading external libraries, modules and so on) that make my life more convenient.
And this concludes my Emacs praise of the day. Thanks for coming.