Solução para a provinha do Google Developer Day 2011 em Python
Esse ano, resolvi tratar com um pouco mais de respeito a prova do GDD. Ano passado, eu resolvi com o prompt do Python aberto, olhando o browser em uma janela e o prompt na outra. Esse ano, as perguntas eram um pouco mais trabalhosas e as strings maiores e isso me fez, em vez disso, escrever um programa. Mais tarde eu coloco o programa no github, mas, por hora, eu transcrevo e comento aqui a minha solução.
A prova apresenta dois textos escritos no idioma Googlon, com os quais vamos trabalhar, e quatro perguntas. Para ajudar (eles são realmente bonzinhos), eles dão as soluções para o primeiro texto, o que ajuda a testar se o código está correto.
Letras foo, bar e preposições
A primeira pergunta explica que algumas letras são chamadas de "letras foo" e todas as demais, "letras bar" e que preposições são palavras de cinco letras que começam com uma letra bar e não contém a letra "q" (é muito provável que a sua prova seja diferente da minha e que elas sejam geradas aleatoriamente - é como eu faria). Para ajudar a resolver, eu escrevi algumas funções
def foo(l):
return l in "snrbg"
def bar(l):
return not foo(l)
def preposicao(p):
return len(p) == 5 and bar(p[-1]) and 'q' not in p
Aí, testar a resposta dada no enunciado é fácil:
>>> palavras_a = texto_a.split(' ')
>>> len(filter(preposicao, palavras_a))
63
Assim como responder a pergunta:
>>> palavras_b= texto_b.split(' ')
>>> len(filter(preposicao, palavras_b))
57
Verbos e verbos em primeira pessoa
A segunda pergunta ensina que verbos são palavras de 6 letras que terminam em uma letra bar. Se ele também começar com uma letra bar, estará em primeira pessoa.
def verbo(p): return len(p) >= 6 and bar(p[-1]) def verbo_primeira_pessoa(p): return verbo(p) and bar(p[0])
Agora podemos testar nosso código com o dado do enunciado:
>>> len(filter(verbo, palavras_a)) == 216 True >>> len(filter(verbo_primeira_pessoa, palavras_a)) == 160 True
E descobrir a nossa própria resposta:
>>> len(filter(verbo, palavras_b)) 224 >>> len(filter(verbo_primeira_pessoa, palavras_b)) 154
No meu caso, eu tinha 224 verbos, dos quais 154 em primeira pessoa.
Vocabulário
Agora o problema pede para criar uma lista com o vocabulário, ordenado segundo o alfabeto googlon. Para isso, eu vou usar o ordenador que já vem embutido nas listas do Python e vou produzir uma função de comparação. Essa função pode ser facilmente plugada em seu próprio sort, se você quiser muito:
def cmp_googlon(p1, p2): v = 'jgptzmqskbclrhdfnvwx' for l1, l2 in zip(p1, p2): if v.index(l1) != v.index(l2): return v.index(l1) - v.index(l2) return len(p1) - len(p2)
E podemos testar com os dados do enunciado:
>>> vocabulario_a_unsorted = list(set(palavras_a)) >>> ' '.join(sorted(vocabulario_a_unsorted, ... cmp = cmp_googlon)) == vocabulario_a True
Nota: ao construir um set com as palavras do texto A, eu eliminei as repetições. Como objetos do tipo set não são ordenáveis, eu transformei o conjunto em uma lista.
Agora podemos encontrar nossa resposta:
>>> vocabulario_b_unsorted = list(set(palavras_b)) >>> vocabulario_b = ' '.join(sorted(vocabulario_b_unsorted, cmp = cmp_googlon)) >>> vocabulario_b 'jgspd jgv jpgzkx jzvjw jmrmlq jmdxx jmntpzq jqw jspk jkc jbb jcphbk jch jcv jlkm...
Números
Agora a prova nos explica que todas as palavras em googlon tem um valor numérico. Em googlon, os números são escritos do dígito menos significativo para o mais significativo e em base 20. Pra isso, precisamos de mais uma função:
def valor_numerico(p): v = 'jgptzmqskbclrhdfnvwx' vn = 0 i = 0 for c in p: vn += v.index(c) * (20 ** i) i += 1 return vn
que, podemos testar contra o enunciado:
>>> valor_numerico('blsmgpz') == 262603029
True
Essa parte está certa. Mas a pergunta pede para contarmos os números bonitos. Para eles, números bonitos são divisíveis por 5 e maiores que 492528.
def numero_bonito(p): return valor_numerico(p) > 492528 and (valor_numerico(p) % 5 == 0)
Agora podemos testar:
>>> len(filter(numero_bonito, vocabulario_a.split(' '))) == 75
True
E chegar na nossa resposta:
>>> len(filter(numero_bonito, vocabulario_b.split(' ')))
71
Conclusão
Foi difícil? Nem um pouco. Se você não conseguiu responder por conta própria, precisa estudar mais. Foi mais trabalhosa do que a do ano passado? Um pouco. Por outro lado, ela tinha informações suficientes para você poder testar suas próprias soluções - e isso ajudou quem teve mais problemas para resolver a prova a aprender alguma coisa. Prova boa é assim - você aprende enquanto faz.
Uma última observação: eu gosto de list comprehensions, mas também gosto de map, filter e reduce. O código fica mais limpo quando eles são bem empregados.
A provinha do GDD, em BASIC (para micros de 8 bits)
Eu confesso que me diverti resolvendo a provinha do GDD. Pra quem chegou agora, foi um teste aplicado pelo pessoal da Google para filtrar inscritos no Google Developer Day. Como eles tiveram muito mais inscritos do que espaço físico comportava, fazia sentido. Embora muitos tenham reclamado, era uma prova muito simples e eu resolvi usando duas linguagens diferentes, Python e Clojure, ambas modernas.
BASIC?!
Um passatempo meu é em paleocomputação, em particular computadores obsoletos, daquelas famílias que não deixaram descendentes diretos. Eu coleciono e, quando possível, restauro, computadores antigos - se você tiver um desses, a propósito, aceito doações. Por isso, eu resolvi brincar um pouco e resolver a provinha do GDD usando um TRS-80 Model III e um Apple II (um //e enhanced, para ser mais preciso). Para tornar a minha vida mais fácil (e evitar um divórcio) eu usei emuladores em vez de computadores reais. Com isso eu pude escrever o código usando um editor de textos de verdade e "colá-lo" no emulador. Em ambas as plataformas, usei seus interpretadores BASIC embutidos na ROM.
Um outro motivo é por esse dialeto de BASIC ser uma linguagem muito mais simples e pobre de recursos do que as duas outras que eu usei nessa brincadeira. Essa simplicidade é visível nas construções que aparecem nesses programas. É interessante notar como os mecanismos de controle de fluxo do programa são mínimos e se mapeiam quase que diretamente ao que o processador entende.
O emulador
A história do emulador é, por si, interessante. Para os dois eu usei o MESS. MESS é uma derivação do MAME que pretende replicar, da forma mais precisa possível, computadores obsoletos. Como os pacotes do Ubuntu me deram algumas dores-de-cabeça, eu compilei a versão mais nova do MESS. Não é difícil e o pessoal do IRC (#messdev na EFNet) foi mais do que gentil e eu teria apanhado muito mais sem eles.
Aliás, quanto a essa coisa de IRC, se vocë desenvolve software e não usa, devia usar. IRC é como um monte de projetos são coordenados, reuniões são feitas e dúvidas tiradas. É normalmente mais rápido que listas de discussão e fórums web. Ache velho e feio por sua conta e risco. Eu não levo a sério nenhum projeto de software aberto que não tenha um canal de IRC com desenvolvedores e usuários conversando.
Mas vamos aos problemas, que são o mais interessante
1) O que esse programa faz?
x = 7 y = 4 if y > 2, then y = y * 2 else x = x * 2 print (x + y)
Em um TRS-80, faríamos assim:
10 X = 7 20 Y = 4 30 IF Y > 2 THEN Y= Y * 2 ELSE X= X * 2 40 PRINT X + Y
Mas isso seria uma estupidez. BASIC (aquele dos anos 70 e 80, pelo menos) é um ambiente interativo - você pode testar idéias de forma rápida e fácil, sem escrever programas. Um programador dos anos 80 faria assim:
X = 7 Y = 4 IF Y > 2 THEN Y= Y * 2 ELSE X= X * 2 PRINT X + Y
E, no seu TRS-80, veria isso:
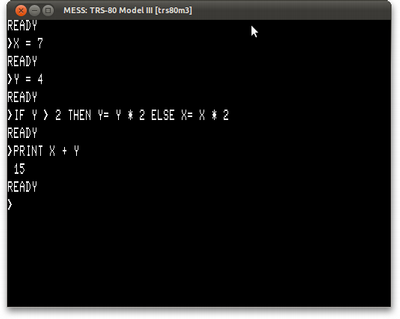
Em um Apple II, por conta do BASIC não ter a palavra ELSE, teríamos que fazer um pouco diferente:
X = 7 Y = 4 IF Y > 2 THEN Y= Y * 2 IF Y <= 2 THEN X= X * 2 PRINT X + Y
E veria algo como
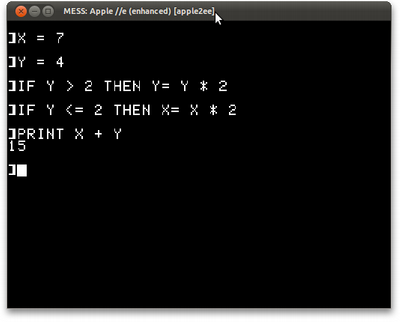
Em forma de programa, no Apple II (e em qualquer caso em que precisássemos de um IF/THEN/ELSE multi-linhas), o jeito típico seria usar um GOTO:
10 X = 7 20 Y = 4 30 IF Y > 2 THEN Y= Y * 2 : GOTO 50 40 X= X * 2 50 PRINT X + Y
E teríamos isso:
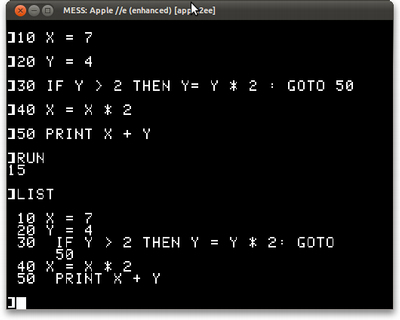
Como a versão BASIC disse "15" e concordou com as versões Python e Lisp, eu me dou por satisfeito.
2) Quantas vezes esse programa imprime "hello"?
for i = 1 to 5
if i != 2, then
for j = 1 to 9
print 'hello'
O programa ficaria assim:
10 FOR I = 1 TO 5 20 IF I <> 2 THEN FOR J = 1 TO 9: PRINT "hello": NEXT 30 NEXT
Sorte nossa o FOR J caber em uma linha.
Ainda assim, estamos com o mesmo problema que tivemos na nossa primeira tentativa (no original em Python) - que é nos obrigar a contar. Um jeito um pouco melhor ficaria assim:
10 FOR I = 1 TO 5 20 IF I <> 2 THEN FOR J = 1 TO 9: C = C + 1 : PRINT C, "hello": NEXT 30 NEXT
Alguém pode perguntar: "Qual é o valor inicial de C?". No BASIC daquele tempo variáveis do BASIC são tipadas pelo nome ("C" só pode representar um número real) e variáveis não inicializadas são zero ou, no caso de strings ("C$", por exemplo) strings vazias. Ou seja, assim que o programa começa a rodar, C é zero - e podemos contar com isso.
Se estiver incomodando muito, mas muito mesmo, digite "5 C = 0" e seja feliz. Não vai fazer mal.
Se fizermos isso no TRS-80, ficaremos com algo assim:
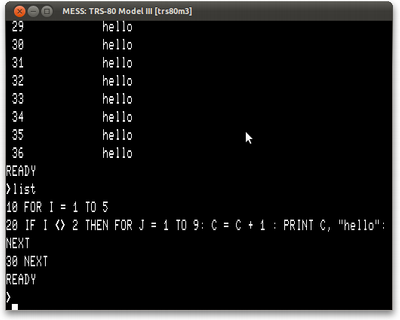

De novo, podemos ficar felizes. O programa em BASIC concorda com os outros - temos 36 (que é a resposta certa, afinal).
3) Quais números, entre 5 e 2675 são pares e divisíveis por 3?
Aqui estamos tão mal quanto o pessoal que fez com Java. Não dá pra fazer nada tão conciso quanto os exemplos em Python e em Clojure. BASIC não tem nenhuma das funcionalidades de geradores de listas que Ruby, Python, Clojure e qualquer linguagem moderna tem.
10 FOR I = 5 TO 2675 20 IF I / 3 = INT(I /3) AND I / 2 = INT(I / 2) THEN C = C + 1 30 NEXT 40 PRINT C
Quando rodar, o programa vai dizer que há 445 números assim.
4) Números bonitos
A pergunta nos apresenta Barbara e seus critérios para que números sejam ou não bonitos. Para ela, números são bonitos se contiverem um dígito 4 e não contiverem um dígito 9. Ao final, nos pergunta quais números entre 14063 e 24779, inclusive, são bonitos.
Esse fica mais complicado. O BASIC que vinha nesses computadores era limitado e não permitia que o programador definisse funções além do mais trivial (uma linha, sem condições). Vamos, por isso, usar uma técnica há muito esquecida (ou que deveria ter sido) que é passar informações por meio de variáveis globais. No caso dos nossos interpretadores, todas as variáveis são globais. Mesmo quem programa em assembly pode contar com a pilha nessas horas. Em BASIC, nem isso.
Você leu direito. Programar naquele tempo não era fácil.
O esqueleto do programa fica assim:
10 FOR I = 14063 TO 24779 20 GOSUB 10000 30 IF B = 1 THEN C = C + 1 40 NEXT 50 PRINT C 60 END
Mas ainda falta o trecho que começa em 10000 que, você deve ter adivinhado, diz se o I é um número bonito e devolve um 1 em B se ele for. O que você vai ver não é bonito para nenhum valor de I, portanto, prepare-se:
10000 REM Primeiro vemos se tem um 4 10010 I$ = STR$(I) 10020 B = 0 10030 FOR J = 1 TO LEN(I$) 10040 IF MID$(I$, J, 1) = "4" THEN B = 1 10050 NEXT 10060 IF B = 0 THEN RETURN 10070 REM Se tem um 4, procuramos um 9 10080 FOR J = 1 TO LEN(I$) 10090 IF MID$(I$, J, 1) = "9" THEN B = 0 10100 NEXT 10110 RETURN
Após um longo tempo, seu computador vai dizer que são 3047 números bonitos:
Nesse ponto, estou começando a achar que eu era mais inteligente nos anos 80. O malabarismo mental de lembrar que variável guarda o que e em que partes do programa essas coisas são alteradas é complicado. E é um bom exercício.
5) Os telefones
A última pergunta nos apresenta um país em que os números de telefone têm 6 dígitos. Números não podem ter dois dígitos consecutivos idênticos, porque isso é caído. A soma dos dígitos tem de ser par, porque isso é legal e o último dígito não pode ser igual ao primeiro, porque isso dá azar.
Vamos começar pelas sub-rotinas. A primeira, para ver se o número de telefone é caído:
10000 REM ve se N$ e caido. Se for, C = 1 10010 C = 0 10020 FOR J = 1 TO LEN(N$) -1 10030 IF MID$(N$, J, 1) = MID$(N$, J + 1, 1) THEN C = 1 10040 NEXT 10050 RETURN
Depois, vendo se ele dá azar:
11000 REM se N$ der azar, A = 1 10010 A = 0 10020 IF LEFT$(N$, 1) = RIGHT$(N$, 1) THEN A = 1 10030 RETURN
E, por fim, se ele é legal:
12000 REM se N$ for legal, L = 1 12010 L = 0: S = 0 12020 FOR J = 1 TO LEN(N$) 12030 S = S + VAL(MID$(N$, J, 1)) 12040 NEXT 12050 IF S / 2 = INT(S / 2) THEN L = 1 12060 RETURN
Vale a pena notar um padrão - como todas as variáveis são globais, é preciso tomar cuidado para que um pedaço do programa não estrague o outro. Nessas subrotinas meu habitual "FOR I" passou a ser "FOR J" para que meu loop da sub-rotina não estrague o loop principal. Eu podia também ter reutilizado o L como acumulador da soma e não estragar o S com isso.
O bloco principal
10 FOR I = 1 TO 200 20 READ N$ 30 GOSUB 10000 40 GOSUB 11000 50 GOSUB 12000 60 IF C = 0 AND A = 0 AND L = 1 THEN Q = Q + 1 70 NEXT 80 PRINT Q 90 END
Só temos um problema - de onde virão os 200 números? O comando READ, na linha 20, lê um valor de uma série de dados literais embutidos no código. Assim, adicionamos uma série de linhas a partir da linha 1000, cada uma com um comando DATA e uma série de strings. Montamos essa linha com um pouco de mágica de copy e paste e busca e troca.
Sim, eu poderia ter pulado os testes depois do primeiro eliminar o número, assim como ter começado com o teste da linha 12000, que é mais simples e rápido. Os algorítmos poderiam ser melhores também e eu poderia ter usado variáveis inteiras onde possível para que os programas rodassem mais rápido.
São 40 linhas com essa cara:
1000 REM Os numeros que precisamos filtrar 1010 DATA "214966", "215739", "220686", "225051", "225123" ... 1400 DATA "715315", "720200", "720202", "720568", "720576"
Quando rodamos o programa, temos a resposta esperada (já fizemos isso algumas vezes, afinal).
TRS-80 e Apple II concordam. 61 parece um bom número.
Isso era mesmo necessário?
Não. Eu não precisava ter feito isso nem mesmo uma vez. A primeira eu fiz porque achei as perguntas interessantes. Muitas e muitas vezes eu já entrevistei pessoas incapazes de escrever um programa de 5 linhas sem ajuda de um Google e, francamente, estou tentado a propor testes formais antes mesmo de um humano colocar os olhos em um currículo. O em Clojure foi motivado pelo contorcionismo sintático de expressar um algoritmo em um cruzamento de Ruby e JavaScript. Esse último veio pelo meu interesse em emuladores, pelo meu interesse em computadores antigos e por eu achar que aprender a programar com um computador de 8 bits é divertido. A simplicidade desses computadores facilita ao novato entender, direito, tudo o que acontece dentro deles nem. Não há compiladores cuidando de você e otimizando código ineficiente. Não há milhares de linhas de código de um kernel distribuindo tempo do processador por dezenas de processos. Tudo é bem simples e acontece do jeito que você mandou.
E, na hora de aprender, simples é bom.
Acho que o próximo precisa ser em FORTH. Vou começar a procurar um dialeto legal pra brincar.
E quanto a você?
Se você quiser brincar com um BASIC antigo, eu recomendo que comece lendo os manuais. Manuais do Apple II e do TRS-80 são fáceis de achar. Outra coisa: eu tomei cuidado de escrever esses programas de modo a eles serem portáteis - você pode usá-los em seu Prológica, Microdigital, ou Unitron. Deve poder rodá-los no seu Atari XL ou no seu Commodore 64. Não testei em todos.
Se você achar a brincadeira (é uma brincadeira - ninguém vai pagar vocë por saber programar um computador de 30 anos de idade) legal, compre um computador antigo e cuide dele. Limpe, conserte. Essas máquinas não vão durar para sempre e marcam o momento importante que essa tecnologia deu: quando deixou de ser aquela máquina que vivia fechada em uma sala e passou a ser aquela que tínhamos em casa. Como disse um especialista da Christies sobre o Apple I que foi leiloado esses dias, "é um pedaço de plástico verde que mudou nossas vidas".
Precisamos cuidar deles.
Mais uma coisa: não me escapou o fato de que esses dois BASICs que eu usei são produtos da Microsoft. Ela fazia coisas bem legais nos anos 70.
A prova do GDD, em Lisp
Outro dia assisti a uma palestra sobre Hadoop e MapReduce. Todos os exemplos foram dados em um pseudocódigo que misturava Ruby com JavaScript enquanto, na minha cabeça, eu os re-escrevia de um jeito que funcionassem de verdade em Python (eu trabalho com isso). Como no meu último post eu já resolvi a provinha do Google Developer Day usando Python (e usei uma função anônima e um filter, vejam só), eu fiquei com a coceira enorme de refazer essas perguntas com Lisp (já que ela expressa maps e reduces como ninguém mais).
No meu laptop eu tenho uns 4 dialetos de Lisp diferentes (não existe uma "implementação canônica" como no caso de Python ou Ruby). Para brincar aqui, eu escolhi Clojure. Clojure é um dialeto de Lisp que roda sobre a máquina virtual do Java (Java é o COBOL do século XXI e provavelmente do XXII, mas a VM e toda a infra-estrutura dela são muito legais). Outro motivo é que o meu Emacs (o IDE to rule them all) está ligado ao Clojure pelo Slime. Eu instalei ambos (Clojure e Slime) com o ELPA, o gerenciador de add-ons do Emacs e, com uma gambiarra e dois symlinks, estou usando o Clojure 1.2 em vez do 1.1 (que é a versão que o ELPA oferece por hora). Eu podia ter tentado usar o Emacs Lisp (o Emacs é quase todo escrito em Emacs Lisp e um REPL dele está sempre disponível), mas ele não é nem um Lisp moderno, nem particularmente gostoso de usar. Podia ter usado Scheme (e provavelmente o resultado seria mais elegante), mas achei que, por rodar na JVM, Clojure é mais "sexy". Qualquer coisa que evite que alguém tenha que escrever código em Java é uma Coisa Boa que merece ser incentivada.
Aqui cabe uma observação: várias linguagens - Scala, Jython, JRuby - permitem que seus programas rodem dentro de máquinas virtuais Java. Todas elas permitem, também, que você use classes que fazem parte tanto do Java propriamente dito como de outros programas nos quais você talvez precise adicionar alguma funcionalidade. A produtividade individual de um desenvolvedor experiente usando uma linguagem como Python e Ruby (dos quais Jython e JRuby são dialetos) já foi observada como sendo superior à de um desenvolvedor igualmente experiente usando Java. Em outras palavras: se você está usando Java você devia dar uma olhada em linguagens mais produtivas.
E isso vale para C#/.NET. Ninguém deveria usar essas tranqueiras.
A propósito, se você quiser ver a resolução da provinha em Jython, vá à outra versão do artigo. É absolutamente a mesma coisa.
Voltando à prova, resolvê-la deu um pouco de trabalho, provavelmente porque eu ainda estou começando a aprender Clojure (o Clojure Programming/Examples/Cookbook e o livro Programming Clojure, de Stuart Halloway tem ambos sido companhia constante aqui - e são bons mesmo como uma introdução ao Lisp - e o The Joy of Clojure é o próximo no wish-list, para assim que estiver pronto) e porque lembro muito pouco de outros dialetos de Lisp (e o pouco que eu lembro, parece, mais atrapalha do que ajuda).
Aviso muito importante: Eu disse isso acima, mas preciso repetir: estou aprendendo Clojure. Posso ter feito alguma barbaridade sem saber. Mais: não fiz qualquer tentativa de otimizar o código exceto para concisão e legibilidade. Também não fiz TDD. E, por favor, não considere meu estilo pessoal como algo que seja bem-vindo (ou mesmo socialmente aceito) entre programadores Lisp ou Clojure. Aceite meus conselhos por sua conta e risco e não me culpe de nada.
Agora que você foi adequadamente avisado, vamos à provinha:
1) O que esse programa faz?
x = 7 y = 4 if y > 2, then y = y * 2 else x = x * 2 print (x + y)
No REPL do Clojure, eu fiz assim:
user> (def x 7) #'user/x user> (def y 4) #'user/y user> (if (> y 2) (def y (* 2 y)) (def x (* 2 x))) #'user/y user> (+ x y) 15
O programa do exercício imprime "15".
2) Quantas vezes esse programa imprime "hello"?
Na linguagem do exercício os loops incluem as extremidades.
for i = 1 to 5
if i != 2, then
for j = 1 to 9
print 'hello'
Vou fingir que, de olhar o pseudocódigo, não dá pra sacar que o programa roda 4 vezes o loop interno e imprime "hello" 36 vezes.
Em Clojure, não temos loops como em Python (ou C, ou quase qualquer outra linguagem desse time). Vamos usar uma list comprehension com o efeito colateral de imprimir coisas na tela.
(for [
i (range 1 6)
j (range 1 10)
]
(if (not= i 2)
(println "hello")
)
)
Ou, de um jeito um pouco mais Clojure, usando a cláusula ":when" no binding dos ranges no lugar do "jeito C de fazer" com o if dentro do bloco:
(for [ i (range 1 6) j (range 1 10) :when (not= i 2) ] (println "hello") )
Executando isso no REPL, ele vai imprimir os "hello"s (como o exemplo em Python fez) entrecortados pelo retorno da list comprehension (que o Python não fez) e isso é chato de contar (ainda mais chato do que o exemplo do Python). Do mesmo jeito que eu fiz com Python, eu vou usar um contador. Como o Clojure abraça a idéia de programação sem efeitos-colaterais e memória transacional, você precisa envolver a coisa cujo estado você pretende alterar em um pouco de burocracia. Famos criar um contador mutável que pode ter seu valor alterado durante a execução do programa.
(def contador (ref 0))
E, com isso, nosso código fica assim:
user> (def contador (ref 0)) (for [ i (range 1 6) j (range 1 10) :when (not= i 2) ] (println (dosync (alter contador inc)) "hello") )
A função "dosync" cuida da transação (eu poderia alterar várias variáveis de uma vez) e "alter" faz a alteração propriamente dita do dado que está na referência "contador". "dosync" nos devolve o resultado da última coisa que ele fez, que foi incrementar o contador. Agora, na janela do REPL, vemos algo como:
32 hello 33 hello 34 hello 35 hello 36 hello nil nil nil nil nil nil nil nil nil nil) user>
Que é exatamente o que nós queríamos. Agora sabemos que o programa imprime "hello" 36 vezes. Se tivéssemos compilado o programa e o executado a partir de um shell, não veríamos os "nil"s (que só são mostrados pelo REPL porque são o retorno de da função println agrupados pelo for - que retorna uma lista com os resultados).
Poderíamos ter sido mais espertos e simplesmente contado o comprimento da lista que o for nos deu (o monte de "nil"s que atrapalha a leitura da nossa saída), mas isso é para o próximo exercício.3) Quais números, entre 5 e 2675 são pares e divisíveis por 3?
O exercício diz que eu posso escrever um programa para isso. Eu não fiz isso com Python e ainda não preciso fazer isso com Lisp. Tenho uma pontinha de dó de quem precisa.
user> (count (for [n (range 5 2676) :when (and (= (mod n 3) 0) (even? n))] n)) 445
Que foi porco da primeira vez e continua porco agora. Quem leu o primeiro post (ou estava acordado no ginásio) sabe que se um número é par e divisível por 3, ele é divisível por 6. Assim, podemos usar o mesmo truque que usamos com Python na nossa solução:
user> (count (for [n (range 5 2676) :when (= (mod n 6) 0)] n)) 445
Eu só sinto saudade da função "even?" da primeira implementação. É legal.
4) Números bonitos
A pergunta nos apresenta Barbara e seus critérios para que números sejam ou não bonitos. Para ela, números são bonitos se contiverem um dígito 4 e não contiverem um dígito 9. Ao final, nos pergunta quais números entre 14063 and 24779, inclusive, são bonitos.
Agora eu vou usar um pedaço do Clojure que não vem carregado, mas que é muito útil: uma biblioteca de manipulação de strings. Para usá-la, vamos fazer:
user> (use 'clojure.contrib.string) WARNING: repeat already refers to: #'clojure.core/repeat in namespace: user, being replaced by: #'clojure.contrib.string/repeat WARNING: butlast already refers to: #'clojure.core/butlast in namespace: user, being replaced by: #'clojure.contrib.string/butlast WARNING: reverse already refers to: #'clojure.core/reverse in namespace: user, being replaced by: #'clojure.contrib.string/reverse WARNING: get already refers to: #'clojure.core/get in namespace: user, being replaced by: #'clojure.contrib.string/get WARNING: partition already refers to: #'clojure.core/partition in namespace: user, being replaced by: #'clojure.contrib.string/partition WARNING: drop already refers to: #'clojure.core/drop in namespace: user, being replaced by: #'clojure.contrib.string/drop WARNING: take already refers to: #'clojure.core/take in namespace: user, being replaced by: #'clojure.contrib.string/take nil
Os warnings dizem que ela mudou o comportamento de algumas coisas que já estavam disponíveis. Não se preocupe com isso: só queremos a função "substring?". Agora, para saber quantos são bonitos, vamos começar com uma função que decide se um número é bonito ou não:
user> user> (defn bonito? [x] (and (substring? "4" (str x)) (not(substring? "9" (str x))) )) #'user/bonito?
Por favor, ignore que eu converti x duas vezes para uma string. Eu otimizo para legibilidade. Outra coisa: eu poderia ter usado .indexOf diretamente ou usá-lo para fazer meu próprio "substring?", mas como clojure.contrib é parte do Clojure, eu acho melhor não duplicar o que é parte do pacote.
Agora temos um "bonito" no nosso namespace. Vamos testá-la, para ver se fizemos tudo direito:
user> (bonito? 4) true user> (bonito? 9) false user> (bonito? 49) false user> (bonito? 1941) false
Daí, basta aplicá-la usando a mesma técnica que usamos no problema anterior:
user> (count (for [ n (range 14063 24780) :when (bonito? n)] n)) 3047
Se você preferir, pode dispensar a função:
user> (count (for [
n (range 14063 24780)
:when (and (substring? "4" (str n))
(not(substring? "9" (str n)))) ]
n))
E tem um jeito ainda mais curto, usando a função "filter".
user> (count (filter bonito? (range 14063 24780))) 3047
E, se eu quiser tornar a coisa um pouco mais obscura usando uma função anônima:
user> (count (filter (fn [n] (and (substring? "4" (str n))
(not(substring? "9" (str n)))))
(range 14063 24780)))
3047
Apesar das aparências, funções anônimas não existem para atrapalhar a legibilidade do seu código mas para que você possa construí-las somente quando necessário e passá-las como parâmetro para outras funções que vão fazer coisas com elas.
5) Os telefones
A última pergunta nos apresenta um país em que os números de telefone têm 6 dígitos. Números não podem ter dois dígitos consecutivos idênticos, porque isso é caído. A soma dos dígitos tem de ser par, porque isso é legal e o último dígito não pode ser igual ao primeiro, porque isso dá azar.
Vamos começar com os caídos. Ao contrário do nosso exemplo em Python, eu preciso me preocupar com os limites dos índices. (nth "abcdef" -1) não é aceitável em Clojure.
user> (defn caido? [n] (some true? (for [i (range (- (count (str n)) 1))] (= (nth (str n) i) (nth (str n) (+ 1 i))) ))) #'user/caido?
Camos fazer alguns testes para ver se estamos encontrando números caídos:
user> (caido? 123456) nil user> (caido? 122345) true user> (caido? 123451) nil
Observe que, ao contrário da solução em Python (que tem um bug, aliás) a função que identifica números caídos não identifica números que não são caídos mas que dão azar como se fossem caídos.
Vamos precisar, então, escrever uma função para os que dão azar. Essa é fácil:
user> (defn da-azar? [n] (= (first (str n)) (last (str n)))) #'user/da-azar?
Só para ter certeza do que fizemos:
user> (da-azar? 123456) false user> (da-azar? 623456) trueE, finalmente, uma para os números legais:
user> (defn legal? [n] (even? (reduce + (map (fn [s] (Integer/parseInt s)) (for [c (str n)] (str c)))))) #'user/legal?
Aqui eu preciso dizer uma coisa: tem que existir um jeito melhor de invocar o método estático parseInt de Integer. Essa cicatriz entre o lado Lisp e o lado Java está muito feia.
Voltando ao exercício, vamos testar nossa função para termos certeza de que não fizemos nada errado:
user> (legal? 12) false user> (legal? 55) trueCom as três na mão, basta usarmos duas no nosso critério:
user> (count (for [n (range 100000 1000000) :when (and (legal? n) (not (da-azar? n)) (not (caido? n)))] n)) 238500
Mas o exercício não perguntou quantos caídos entre 100000 e 999999. Eles nos deu uma lista. Com um pouco de mágica de clipboard, colocamos os números em uma string, que quebramos e fazemos uma lista:
user> (def tudo "214966
215739
220686
225051
225123
(...)
720202
720568
720576
")
#'user/tudo
user> tudo
"214966\n215739\n220686\n225051\n225123\n...720202\n720568\n720576\n"
user> (def numeros (split-lines tudo))
#'user/numeros
user> numeros
("214966" "220686" "225051" "225123"..."720202" "720568" "720576")
user> (count numeros)
200
Então, usamos a lista e chegamos no resultado:
user> (count (for [n numeros :when (and (legal? n) (not (da-azar? n)) (not (caido? n)))] n)) 61
61 de 200 é o resultado que tivemos antes. Se erramos, erramos duas vezes do mesmo jeito.
Não doeu tanto assim, doeu?
Muitos programadores morrem de medo de Lisp. Morrem de medo, vêm um monte de parênteses, acham confuso e desistem. Lisp é uma linguagem muito interessante - a mais antiga ainda em uso - e impõe uma certa disciplina que é útil para qualquer programador. Robert "Uncle Bob" Martin recomenda que todo programador profissional aprenda uma linguagem "diferente" das que conhece por ano. A analogia que ele faz é interessante: um carpinteiro que só sabe fazer banquinhos de pinho não é um bom carpinteiro. Ele precisa aprender a trabalhar com outros tipos de madeira e a fazer outros tipos de móvel.
Se tudo o que você sabe fazer são sites em PHP ou módulos de ERP em C#, talvez seja hora de pensar em aprender algo novo.
A "provinha" do Google Developer Day
Algumas pessoas acharam estranho o processo de inscrição para o Google Developer Day. Nas edições anteriores, você preenchia um formulário, contava o que você fazia e onde trabalhava e ficava nisso. Os primeiros a se inscreverem iriam ao evento e pronto. Os menos atentos ganhavam a lista de espera. Agora, além do formulário, você tem que mandar um currículo e resolver alguns problemas que exigem familiaridade com alguma ferramenta de programação.
Não sei se foi essa a intenção da Google, mas, com esse processo de inscrição, eles têm seus dados de contato, seu currículo e sua avaliação em uma prova.
Mas não se anime. Essa prova não deve ser a que o RH do Google usa. Eu, pessoalmente, acredito que ela apenas existe para separar quem vai entender alguma coisa do GDD de quem não vai entender nada e evitar, com isso, que gente que poderia melhor aproveitar o evento fique de fora.
Agora que as inscrições foram fechadas e o prazo para a entrega das provas terminou, eu me sinto à vontade para publicar esse post.
A prova
A prova tem 5 questões, um pouco diferentes para cada candidato. Eu não sei se foi honesto, mas eu resolvi as minhas com uma janela e um interpretador Python do lado. E eu vou fazer o mesmo aqui.
O que esse programa faz?
x = 7 y = 4 if y > 2, then y = y * 2 else x = x * 2 print (x + y)
Esse é facil. Na janela do ipython:
In [1]: x = 7 In [2]: y = 4 In [3]: if y > 2: ...: y = y * 2 ...: else: ...: x = x * 2 ...: ...: In [4]: x + y Out[4]: 15
Quantas vezes esse programa imprime "hello"?
Uma observação: os loops incluem as extremidades.
for i = 1 to 5
if i != 2, then
for j = 1 to 9
print 'hello'
De novo, com o mesmo truque (só que em Python, o range não inclui a extremidade maior):
In [1]: for i in range(1, 6): ...: if i != 2: ...: for j in range(1, 10): ...: print 'hello' ...: ...: hello hello hello hello ...
Erm... Chato assim. Vamos tentar de outro jeito
In [1]: linha = 1 In [2]: for i in range(1, 6): ...: if i != 2: ...: for j in range(1, 10): ...: print linha, 'hello' ...: linha += 1 ...: ...: 1 hello 2 hello 3 hello 4 hello (...) 36 hello
Agora sim. Mesmo sem o computador, de olhar dá pra sacar que o primeiro loop roda 5 vezes e o segundo, 9. Como a condição que pula o segundo loop pula uma iteração (nem todos os testes fazem isso), o programa imprime 4 x 9 hello's.
Quais números, entre 5 e 2675 são pares e divisíveis por 3?
O exercício diz que eu posso escrever um programa para isso. Deve ser pra acomodar o pessoal que não vive sem um compilador.
In [1]: len([ n for n in range(5, 2676) if n % 2 == 0 and n % 3 == 0 ]) Out[1]: 445
Mas isso foi porco. Quem estava acordado no ginásio vai lembrar que se um número é par (divisível por 2 - essa é do primário) e divisível por 3, ele é divisível por 6. Assim, podemos simplificar nossa solução:
In [2]: len([ n for n in range(5, 2676) if n % 6 == 0 ]) Out[2]: 445
Podemos respirar aliviados agora que vimos que o resultado continua o mesmo.
Números bonitos
A pergunta nos apresenta Barbara e seus critérios para que números sejam ou não bonitos. Para ela, números são bonitos se contiverem um dígito 4 e não contiverem um dígito 9. Ao final, nos pergunta quais números entre 14063 and 24779, inclusive, são bonitos.
Para saber quantos são bonitos, podemos começar com uma função:
In [1]: def bonito(x): ...: return '4' in str(x) and '9' not in str(x) ...:
E podemos testá-la, para ver se fizemos tudo direito:
In [2]: bonito(4) Out[2]: True In [3]: bonito(9) Out[3]: False In [4]: bonito(49) Out[4]: False In [5]: bonito(1491) Out[5]: False
Daí, basta aplicá-la usando a mesma técnica que usamos no problema anterior:
In [6]: len([ n for n in range(14063, 24780) if bonito(n) ]) Out[6]: 3047
Se você preferir, pode fazer tudo em uma linha:
In [7]: len([ n for n in range(14063, 24780) if '4' in str(n) and '9' not in str(n) ]) Out[7]: 3047
Ou, ainda:
In [8]: len(filter( lambda x: '4' in str(x) and '9' not in str(x), range(14063, 24780))) Out[8]: 3047
Os telefones
A última pergunta nos apresenta um país em que os números de telefone têm 6 dígitos. Números não podem ter dois dígitos consecutivos idênticos, porque isso é caído. A soma dos dígitos tem que ser par, porque isso é legal e o último dígito não pode ser igual ao primeiro, porque isso dá azar.
Vamos começar com os caídos
In [1]: def caido(x): ...: for i in range(0, len(str(x))): ...: if str(x)[i] == str(x)[i - 1]: ...: return True ...: return False ...:
Agora vamos para os legais
In [2]: def legal(x): ...: return sum([ int(n) for n in str(x) ]) % 2 == 0 ...:
E, se olharmos a função "caido", vamos ver que ela considera caídos os números que dão azar.
In [3]: caido(123451) Out[3]: True
Assim, basta usarmos duas no nosso critério:
In [4]: len([ n for n in range(100000, 1000000) if not caido(n) and legal(n) ]) Out[4]: 238500
Mas o exercício não perguntou quantos caídos entre 100000 e 999999. Eles nos deu uma lista. Com um pouco de mágica de clipboard, colocamos os números em uma string, que quebramos e fazemos uma lista:
In [5]: tudo = '''214966 ...: 215739 ...: 220686 ...: 225051 ...: 225123 ...: 226810 ...: 228256 (...) ...: 720576 ...: ''' In [6]: tudo Out[6]: '214966\n215739\n220686\n225051\n225123\n...720202\n720568\n720576\n'
Opa! Tem um '\n' no final do qual precisamos nos livrar
In [7]: numeros = tudo.split('\n')[:-1]
In [8]: len(numeros)
Out[8]: 200
Então, usamos a lista e chegamos no resultado:
In [9]: len([ n for n in numeros if not caido(n) and legal(n) ]) Out[9]: 61
61 de 200 parece razoável.
Motivo para pânico?
Não desanime se seus números forem muito diferentes dos meus. Os enunciados variam de teste para teste. Além disso, até agora eu não recebi confirmação da minha inscrição. Isso pode indicar que eu errei tudo.
Boa sorte!